Posted on

Predicting Mechanical Response of SLS PA11 Structures

One of the key value propositions for additive manufacturing is to create mechanically superior parts using complex geometric structures, such as the gyroid shown below. While complexity may be “free” from a processing point of view, taking advantage of this complexity in a useful way requires both sophisticated knowledge of the mechanical behavior of the selected material and expertise in modeling non-linear materials and structures. This case study highlights what is involved in simulating a complex additively manufactured structure. We have chosen SLS polyamide 11 (PA11) as the material, but the considerations are the same regardless of process/material combination.

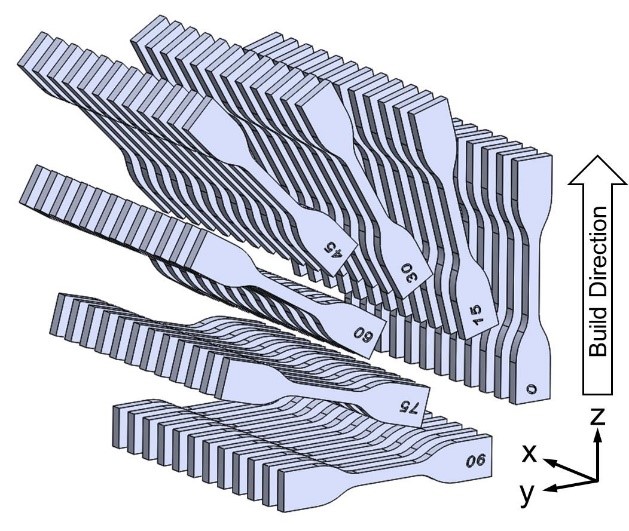
To begin, accurate mechanical analysis requires knowing the stress-strain response of the material under the relevant loading conditions. Mechanical properties listed on data sheets are useful for comparative purposes but are not sufficient for simulation-based design. To get the experimental data needed for an accurate model, we conducted a series of experiments to characterize the influence of loading mode (tension/compression), build orientation (θ), and strain rate (ἑ), on the mechanical behavior of SLS PA11.

The experimental data is shown in the figure below up to engineering strains of ±20%. We measured the orientation-dependent tensile response and found the elastic and yielding behavior to be effectively isotropic. From a design point of view, this greatly simplifies things because many additively-manufactured polymers exhibit anisotropic yield properties which must be subsequently modeled. We also measured the compressive stress-strain response at three strain rates to characterize the rate sensitivity of the material. The PA11 exhibited moderate rate dependence and asymmetry in the yield point between tension and compression.

To model the deformation of this material, we chose the three-network model from the PolyUMod® library of advanced user materials (www.polyumod.com), which was developed specifically for thermoplastics. The model was calibrated to the experimental data using MCalibration®. The figure below shows the calibrated material model plotted as heavy dashed lines. The model accurately captures the measured stress-strain behavior, including the rate-dependence and the difference in yielding between tension and compression.

Finally, using the calibrated three-network model for PA11, we simulated the deformation of the gyroid shown above using finite element analysis (FEA). The 3D mesh required for the FEA was generated using a custom meshing tool developed at Veryst Engineering. A snapshot of the simulation is shown below with the contours representing the magnitude of the von Mises stress that develops in the structure under uniaxial strain.

The predicted stress-strain response of the structure under uniaxial strain is shown below. Note the asymmetry in the non-linear regions. In tension, the structure is predicted to harden after yielding, whereas in compression, the stress is predicted to plateau until self-contact starts to occur.

In summary, advances in AM processing, simulation, and design will continue to enable the fabrication of increasingly complex end-use parts. Strategic mechanical testing, state-of-the-art material modeling, and non-linear FEA are all critical to enabling these advances.

Posted on

Anisotropy of SLS PA12

One of the challenges of designing with AM polymers is accounting for their anisotropic mechanical properties. These materials frequently fail more easily when loaded along the build direction due to weak interlayer bonding. An engineer could conservatively assume the weakest properties for every orientation, but this assumption counters the goal of using AM to enable highly-optimized part geometries. Therefore, maximizing AM part performance requires a detailed understanding of this mechanical anisotropy exhibited by AM polymers.

We characterized the mechanical anisotropy of polyamide 12 processed by selective laser sintering (SLS). The mechanical properties of AM materials are often reported in only the 0° and 90° degree orientations. These data alone do not fully describe the material anisotropy. To build a complete description of how material properties depend upon the loading orientation with respect to the build direction, we printed and tested tensile specimens at seven orientations, as shown in Figure 1.

Figure 1. Tensile specimen orientations

We tested the printed SLS specimens to failure in tension using full field digital image correlation (DIC) to measure strain.  Figure 2 presents the stress-strain curves of the weakest and strongest specimens in the study. The inset image shows a representative DIC strain field captured during the experiments. Interestingly, the material performed best when loaded at 60°, not 90°, with respect to the build direction.

Stress-Strain Response

Figure 2. Representative stress-strain curves

Figure 3 shows how the true stress and true strain at failure varied with build orientation. The points represent the mean measured values and the error bars denote the minimum and maximum measured values for nine tests. The trends in the data are well-captured by the models shown as dashed lines in Figure 3.

Figure 3. True stress and strain at failure as a function of build orientation

When possible, engineers should work to align the stresses in a part with the strongest material orientation.  As an illustration of why this is important, we printed a lattice structure in different orientations and loaded the parts to failure in three-point bending (Figure 4).  Consistent with the tensile test data, the structural performance was maximized by printing the part such that the max principal stress was oriented ~60° to the build direction.  By optimizing the build orientation, the energy required to break the part increased by 58% compared to the 0° orientation, and 16% compared to the 90° orientation.

Bend testing of a lattice structure

Figure 4. Energy required to break an SLS lattice structure in bending as a function of build orientation